
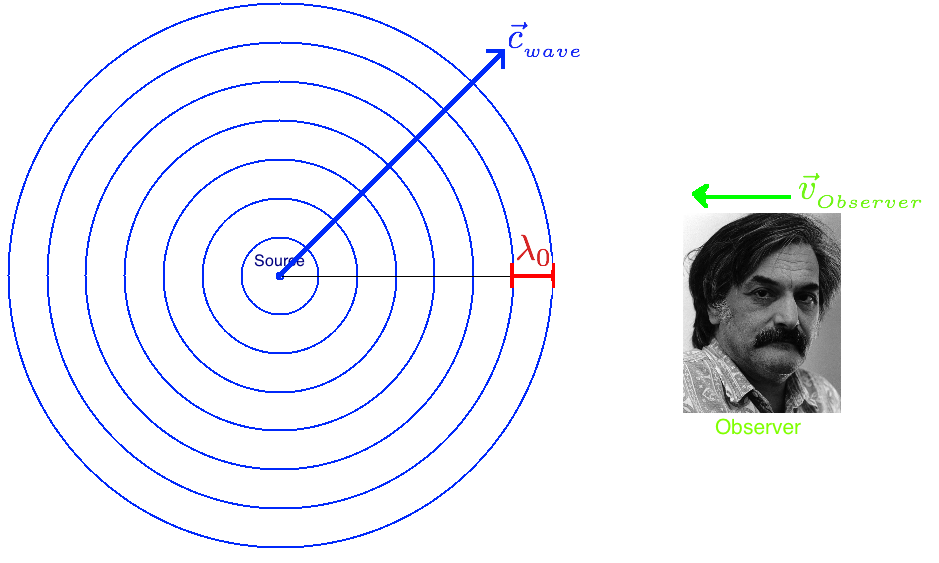
As we saw in lecture 3 of week 4 (Of Hummingbirds, Trains, and the Doppler Shift), the frequency of a wave increases when either an observer is moving toward a source or the source is moving towards the observer (or both). For the simplest derivation of the Doppler shift formula, we will examine the case where our observer is moving with velocity $\vec{v}_{_{observer}}$ towards a stationary source that generates waves with wavelength $\lambda_0$. In this instance, waves travel radially and concentrically outward from our source at a velocity $\vec{c}_{_{wave}}$.
If we imagine that each of the blue concentric circles in the image below, represents the peak of a wave, we see that the observer will encounter waves with a higher frequency (i.e. more waves per unit time) since the observer is moving directly into the wave, thus encountering peaks more quickly than would happen if he or she were stationary. This situation is analogous to a jet-skier that is riding into the water waves, where the ride is arguably much rougher than when the jet ski was standing still.
When both the source and the observer are standing still, in time "t", a wave will traverse a distance of $\vec{c}_{_{wave}}\times t$. If the wavelength of the signal (sound, water, light, etc.) is $\lambda_0$, then the observer will see (or hear) "N" waves pass by, where $$N_{_{waves}}=\frac{c_{_{wave}}\;t}{\lambda_0}.\:\:\:\left(1\right)$$ (Note that we drop the vector notation for velocity of the wave ($c_{_{wave}}$), since only the magnitude, or speed, is relevant here).

If however, the observer is moving toward the source at a speed of $v_{_{observer}}$, he will travel an additional distance of $d=v_{_{observer}}\times t$. This means that we would now encounter an additional number of waves:$$\Delta N_{_{waves}}=\frac{v_{_{observer}}t}{\lambda_0}\:\:\:\left(2\right)$$ for a total of $\Delta N_{_{waves}}+N_{_{waves}}=N_{_{waves}}^{\prime}$ waves. Thus, by dividing through by the time interval $t$, we recast our formula in terms of frequencies:$$\frac{\Delta N_{_{waves}}}{t}+\frac{N_{_{waves}}}{t}=\frac{N_{_{waves}}^{\prime}}{t}\Longrightarrow$$ $$\Delta f+f_0=f^{\prime}, \:\:\:\:\:\:\:\left(3\right)$$
where $f^{\prime}$ is now our new observed frequency when we approach the source.
Now we can express $f^{\prime}$ using eqn. (2) as follows: $$f^{\prime}=f_0+\Delta f$$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{c_{_{wave}}}{\lambda_0}+\frac{v_{_{observer}}}{\lambda_0}$$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\frac{c_{_{wave}}}{\lambda_0}\left(1+\frac{v_{_{observer}}}{c_{_{wave}}}\right)$$ $$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=f_0\left(1+\frac{v_{_{observer}}}{c_{_{wave}}}\right).\:\:\:\:\:\:\:\left(4\right)$$ It is important to note that $v_{_{observer}}$ is negative if the observer is moving away from the source of waves.
Try your hand at combining eqns. (3) and (4) to show that the formula ($\frac{\Delta f}{f_0}= - \frac{v}{c}$) written on the blackboard of the lecture video (at about the 6:00 minute mark) follows immediately. (And thereby answer the question: why is there a "minus" sign on the blackboard, and NOT on this page?)
The equations for when the source is moving (or both source and observer are moving) turn out to be somewhat different, but it is interesting and important to note that when $v_{_{source}}\lt\lt c_{_{wave}}$ and/or $v_{_{observer}}\lt\lt c_{_{wave}}$, the results reduce to the same expression as given in eqn. (4).